注意

这是一篇让AI总结的论文精读，我只做了简单的修正和补充。可能存在错误或不准确的地方。

论文：Learning to Reason in 13 Parameters
arXiv：2602.04118
主题：参数高效微调（PEFT）与强化学习（RL）
screenshot
中文翻译版：2602.04118
翻译SKILL: yrom/arxiv-paper-translator

一句话总结（TL;DR）

TinyLoRA 用 LoRA-XS + 随机投影 + 权重绑定把可训练参数压到 13 个，配合 GRPO 在 GSM8K 评测集上跑分从 76% 提到 91%。关键发现：强化学习（RL） 的稀疏可验证信号比监督微调（SFT）的逐 Token 信号更适合采用极低参数的设置。

1. 直觉开场：13 个参数？

如果把全量微调看成”重装整台电脑”，那 LoRA 像”换一条内存条”，TinyLoRA 则更像”在 BIOS 里拨了 13 个开关”——改动极小，但让模型更愿意”想一想、写长一点”，推理准确率就上来了。

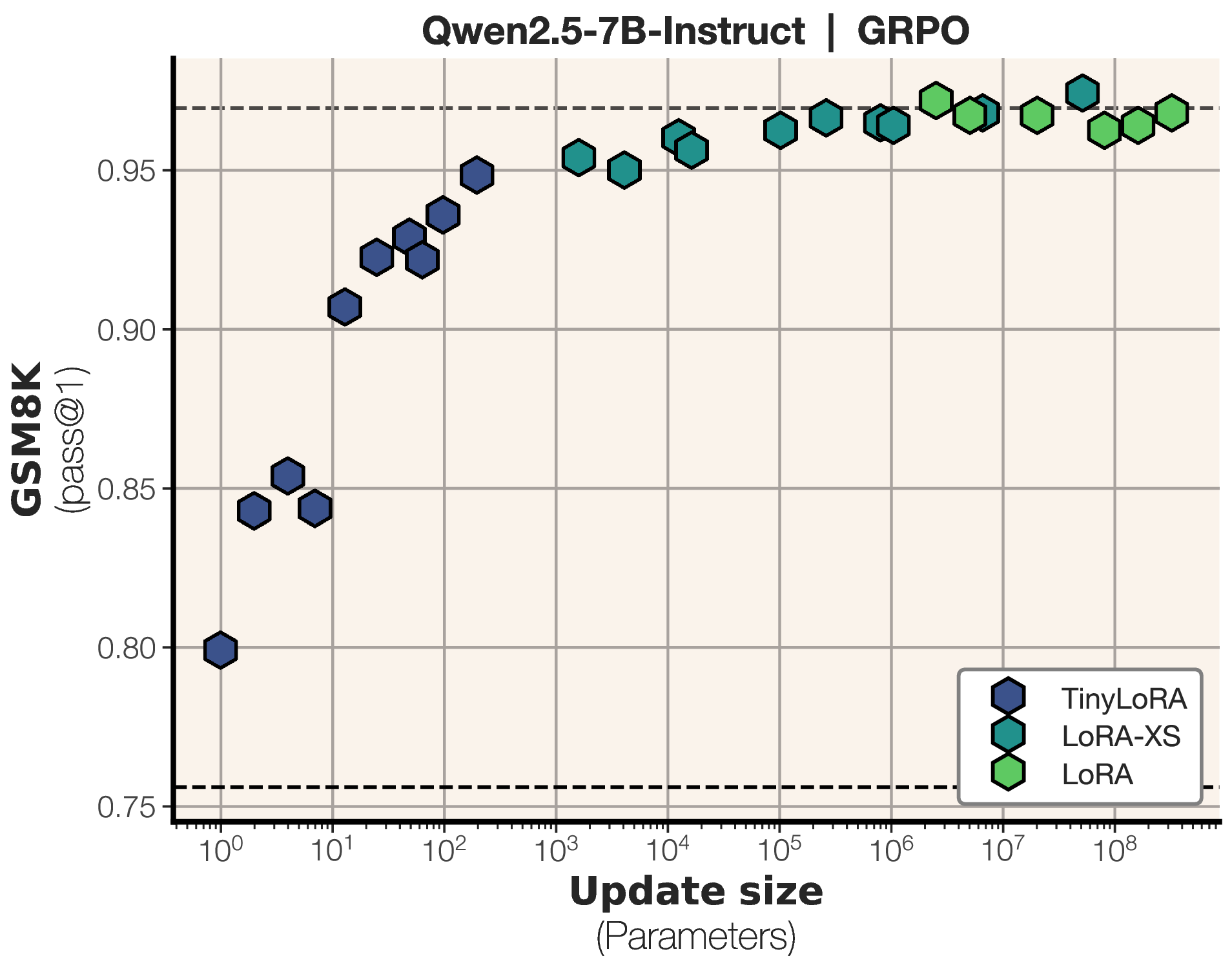
图1：GSM8K 上 TinyLoRA + GRPO 在 13 参数下接近全量微调
图1：GSM8K 主结果（GRPO）。13 参数即可逼近全量微调性能，虚线为未训练与全量微调基线。

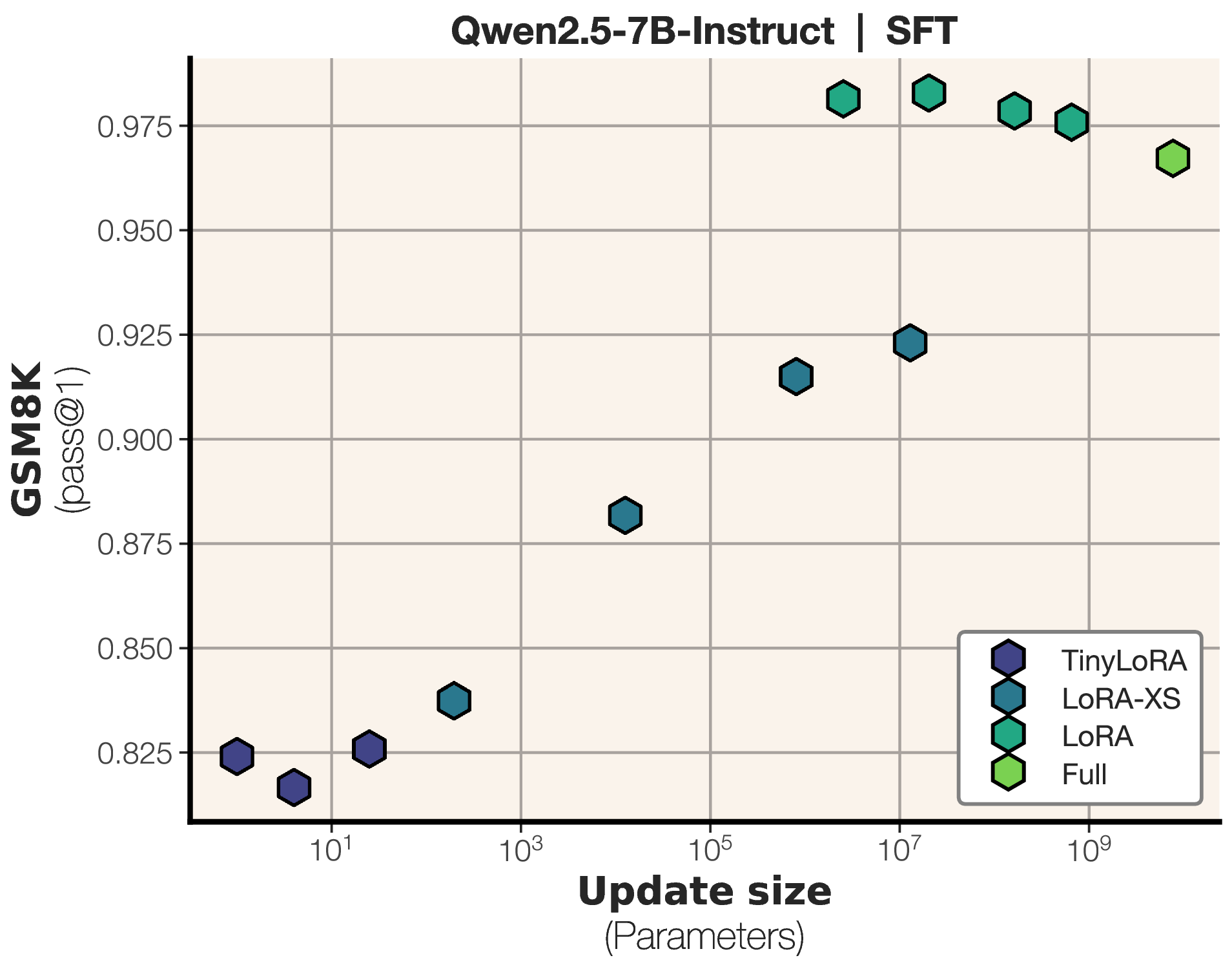
图2：SFT 在 GSM8K 上需要更大的更新规模
图2：SFT 在低参数区间效果明显弱于 RL，达到相近性能需要更大的更新规模。

2. 背景：为什么 LoRA 还不够高效？

LoRA (Hu et al., 2021, arxiv:2106.09685) 把权重更新写成低秩矩阵，并给出了一个可控的“参数预算—性能”通道：

W′=W+ABW' = W + AB

其中，$W$ 为冻结的原始权重，$A \in \mathbb{R}^{d \times r}$、$B \in \mathbb{R}^{r \times k}$ 为可训练的低秩更新矩阵。该式体现了 LoRA 的核心思想：用一个低秩增量近似原始权重的更新，从而把可训练参数量从 $\mathcal{O}(dk)$ 降到 $\mathcal{O}(dr)$。

在此基础上，LoRA-XS (Bałazy et al., 2025, arxiv:2405.17604)：

W′=W+UΣRVTW' = W + U \Sigma R V^T

其中 $U \in \mathbb{R}^{d \times r}$、$\Sigma \in \mathbb{R}^{r \times r}$和$V \in \mathbb{R}^{k \times r}$ 来自 $W$ 的截断 SVD 且保持冻结，仅训练 $R \in \mathbb{R}^{r \times r}$，使每模块参数量降为 $\mathcal{O}(r^2)$。

截断 SVD 的含义：对 $W$ 做奇异值分解 $W = U\Sigma V^\top$，仅保留前 $r$ 个最大的奇异值及其对应的奇异向量，得到 $U_r,\Sigma_r,V_r$。这等价于用最重要的 $r$ 个“主方向”近似 $W$，从而把更新自由度压缩到 $r$ 维。

图3：LoRA 与 LoRA-XS 对比
图3：LoRA 与 LoRA-XS 对比。LoRA-XS 仅需训练一个小矩阵 $R$

问题是：
尽管 LoRA/LoRA-XS 显著降低了可训练参数，但参数下限仍与“模块数量与模型规模”强绑定。即便在 $r=1$ 的极限下，LoRA-XS 也至少需要“每模块一个参数”，在大模型上仍是数百级的更新量。
于是核心问题变成：能否把更新规模压到十几甚至个位数，并在合理训练范式下保持有效性能？ TinyLoRA 就是在这一问题上向极限推进的尝试。

3. TinyLoRA 的核心思路与方法推导

3.1 参数化压缩路径：LoRA → LoRA-XS → TinyLoRA

LoRA 与 LoRA-XS 的参数化形式分别为：

LoRA: W’=W+ABLoRA-XS: W’=W+UΣRV⊤\begin{aligned}
\text{LoRA: } & W’ = W + AB \
\text{LoRA-XS: } & W’ = W + U \Sigma R V^\top
\end{aligned}

TinyLoRA 的思路是，把 LoRA-XS 的小矩阵 $R$ 进一步压缩为低维向量的随机投影：

W′=W+UΣRVT=W+UΣ(∑iviPi)VT\begin{aligned}
W’ & = W + U \Sigma R V^T \
& = W + U \Sigma \left( \sum_i v_i P_i \right) V^T
\end{aligned}

其中 $P_i \in \mathbb{R}^{r \times r}$ 为固定随机矩阵，$v \in \mathbb{R}^{u}$ 为可训练向量。单模块参数为 $u$。

再引入参数共享（parameter sharing）或者说权重绑定（weight tying），使多个模块共享同一 $v$：

Nparams=nmuntieN_{\text{params}} = \frac{n m u}{n_{\text{tie}}}

其中 $n$ 是模块数量，$m$ 是每模块参数量（与秩 $r$ 相关），$u$ 是每模块可训练向量维度，$n_{\text{tie}}$ 是共享的模块数量。

当 $n_{\text{tie}}=nm$（全量共享）时，总参数量降到 $u$；
在 $u=1$ 的设置下，意味着总训练参数仅为 $1$，即所有模块共享同一个可训练向量 $v$。

For a model like LLaMA-3 70B with 80 layers, even the minimal case of $u=1$ requires $80 \times 7 = 560$ trainable parameters. With full weight tying ($n_{\text{tie}}=nm$), all modules share a single $\mathbf{v}$, reducing the total to just $u$ parameters—as few as one.

表：TinyLoRA 压缩参数
表：压缩参数对比。

3.2 学习信号与容量：SFT vs RL

将模型记为 $\pi_\theta$，输入 $x \in \mathcal{X}$，输出 $y \in \mathcal{Y}$。

SFT 的目标为：

LSFT(θ)=−E(x,y)∼(X,Y)[∑t=1∣y∣log⁡πθ(yt∣x,y<t)]\mathcal{L}{\text{SFT}}(\theta) = -\mathbb{E}{(x,y) \sim \mathcal{(X,Y)}} \left[ \sum_{t=1}^{|y|} \log \pi_\theta(y_t \mid x, y_{<t}) \right]
RL的策略梯度更新为：

∇θJ(θ)=Ex∼X; y∼πθ[∑t=1∣y∣∇θlog⁡πθ(yt∣x,y<t)⋅R(y)]\nabla_\theta J(\theta) = \mathbb{E}{x \sim \mathcal{X};\ y\sim \pi_\theta} \left[ \sum{t=1}^{|y|} \nabla_\theta \log \pi_\theta(y_t \mid x, y_{<t}) \cdot R(y) \right]
其中，SFT 的目标是最大化给定输入 $x$ 时正确序列 $y$ 的对数似然；模型在每个时间步 $t$ 都被监督去拟合 $y_t$，因此损失函数在每个 token 上都有直接梯度。

RL 的期望则包含“策略采样”过程：给定 $x$，输出 $y$ 是从当前策略 $\pi_\theta$ 采样得到的。
梯度项 $\nabla_\theta \log \pi_\theta(y_t \mid x, y_{<t})$ 在每个时间步出现，但整体被同一个奖励 $R(y)$ 统一加权，表示“这条序列整体好不好”。

论文作者认为这两者关键差异在于信息结构：

  • RL 的有效信息主要集中在奖励上，每个 Prompt 的有效信息量上界为 $k \cdot H(\mathcal{R})$（二值奖励时上限为 $k$），信号“稀疏但纯粹”；
  • SFT 则在每个 Token 上都需要施加梯度，信号密集且混杂，低参数容量下难以分离有用信息与分辨噪声。

RL presents more data but less information.
…The relevant information lies entirely in the reward, which is only $k \cdot H(\mathcal{R})$ bits per prompt—bounded by $k$ when the reward is binary.…
…Without a mechanism to separate signal from noise, SFT must treat all tokens as equally informative, storing both the useful structure and the irrelevant details.

比喻理解

  • SFT 像"单词听写"：每个 token 都要记，参数少的时候就是笔记本太小，记不全。
  • RL 像"判卷"：只看最终答案对不对，不要求你复述解题过程。 RL 的有效信息集中在奖励 $R$ 上，信息量随采样数 $k$ 线性增长，但不随序列长度膨胀；SFT 的损失则在每个 token 上产生梯度，信号密集且混杂。所以在极低参数时，RL 的信号更容易被少量参数承载。

3.3 合并理解

TinyLoRA 的可行性来自这两个条件的叠加：其一是参数化压缩把可训练参数压到极小；其二是 RL 的奖励信号相对稀疏且可分离，使少量参数仍能对性能产生稳定影响。

换言之，它是在激活模型中已有的结构，而非凭空创造新的能力。

4. 实验主线：从 13 参数到更难任务

4.1 GSM8K 主结果

13 个 bf16 参数（26 字节）让 Qwen2.5-7B-Instruct 从 76% 提升到 91%。
同样 13 参数下，SFT 只有 83%。

实验采用 GRPO 进行强化学习，并使用精确匹配（exact-match）奖励作为反馈信号。

4.2 更难基准（MATH / AIME / AMC）

在更难的数学基准上，即便只训练 196 个参数，性能仍保留了全量微调 87% 的提升。

图3：MATH 训练过程的平均奖励与响应长度
图3：MATH 训练过程的平均奖励与响应长度变化，体现小更新规模也能逐步提升奖励与响应长度。

表：Performance on math reasoning using Qwen2.5 models.
表：Qwen2.5 系列模型在 MATH 基准上的表现对比，(0)为未训练基线，(*数字)为全量微调（no LoRA）；所有实验使用 GRPO，训练 3 个 epoch。

5. 模型规模与更新量：大模型更”省参数”

模型越大，达到同样性能所需的更新参数反而越少。

图4：不同模型规模下 TinyLoRA 在 GSM8K（GRPO）上的表现
图4：TinyLoRA 在不同背骨规模上的表现，虚线为未训练基线；小更新主要在更大模型上带来提升。

图5：达到性能阈值所需的最小更新规模随模型变大而下降
图5：更大模型达到固定性能阈值所需的更新规模更小，显示参数效率随模型规模提升。

论文还指出，在相同更新规模下，Qwen 系列在小参数区间明显优于 LLaMA 系列，达到同等性能所需参数量约少 10 倍。

6. 消融实验：参数该怎么”花”最值？

6.1 冻结秩 r 的选择

结果出人意料：r=2 最优。
直觉上更多秩意味着更强表达力，但在 TinyLoRA 的低参数设置下，秩高了反而不好训。

图6：冻结秩 r 与可训练秩 r_trainable 的二维消融
图6：冻结秩与可训练秩的组合影响，显示低参数预算下的最佳配置区域。

6.2 绑定层数 vs 参数独立性

共享能省参数，但共享过度会导致各层失去区分度。
实验表明，更少共享、更多独立参数更有效。

图7：不同绑定层数与秩 r 的性能消融（3B 规模）
图7：3B 模型上不同绑定层数与秩 r 的性能对比，显示共享程度与秩的耦合影响。

图8：不同绑定层数与可训练秩的消融
图8：绑定层数与可训练秩的组合影响，提示应优先“扩展 u 再增加共享”。

6.3 精度与共享策略

令人意外的是，fp32 在按字节效率上反而优于低精度格式——每个参数占的字节多了，但携带的有效信息也更多。

图9：共享策略与精度的消融（小于 1KB 更新规模）
图9：共享策略与数值精度的消融，fp32 在按字节效率上表现更好。

7. 总结

这篇论文的核心贡献是实验证明了：在 RL 训练范式下，极少量参数（低至 13 个）就足以激活大模型已有的推理能力。参数量不是瓶颈，训练信号的质量才是。

目前论文只验证了数学推理场景（奖励信号天然二值、可自动验证）。对于开放式对话、写作这类难以定义清晰奖励的任务，TinyLoRA 的极端参数效率是否还能保持，是一个值得继续追的问题。

References

Author: Yrom

Link: https://yrom.net/blog/2026/02/10/paper-reading-tinylora/

License: 知识共享署名-非商业性使用 4.0 国际许可协议